先日、ときどきは小学生~高校生レベルの話題を取り上げるという話をしましたが、今回もそういった内容です。
ネット上でいろいろな方の意見を見ていると、「今どきのコンピュータは高速で、コンパイラの最適化性能も上がっているので手作業で最適化する必要などない」という声が少なくありません。この意見は必ずしもまちがってはいませんが、あてはまる状況は限られています。
PCをはじめとするハイエンドな環境であればその通りでしょう。しかし、現在でもまだ8ビット以下のプロセッサは現役で使われていますし、32ビット程度のプロセッサであってもFPU(浮動小数点ユニット)がないとか、コンパイラの最適化性能が残念だったりとかということは普通にあるのです。
また、「“時期尚早な最適化”は諸悪の根源だ」という主張も目にします。これは確かにその通りです。しかし、本当に最適化すべき時期が来たときに手作業で最適化する技術がないとなれば、これは困ったものです。
というわけで、今回は最適化の話を少ししてみます。といっても、特定のプラットフォームや言語に特化した話をするつもりはありません。今回お話しするのは数値演算についてです。
わかりやすい例として、二次方程式の解の公式を考えてみることにします。
$$x=\frac{-b+\sqrt{\mathstrut b^2-4ac}}{2a}$$
中学校で習ったおなじみの式ですね。 本当は二次方程式の解は2つありますが、ここでは話を簡単にするために片方だけにしぼって話をすることにします。
この式を素直にプログラミング言語で実装することは簡単ですし、実際のところそれで済んでしまうことも少なくありません。しかし、FPUのないマイコンで、コンパイラの最適化性能は非常に低いにもかかわらず、頻繁にこの式を計算しないといけないとしたらどうでしょう。場合によっては必要な要件を満たせなくなることもあります。
そうした場合、顧客に要件を緩和してもらう交渉をするのも一案ですが、できれば本来の要件を満たせるように最適化したいものです。
手作業で最適化する手法はいろいろ考えられます。まず、頻繁に計算するとはいっても、毎回値が変化するパラメータとそうでないものがあるかもしれません。もし、cは毎回変化するけれども、aとbは初回に値を決定すれば以降は変わらないとしたらどうでしょう?
次のように式を変形することで、値が毎回変化する部分と変化しない部分を分離してみることにしましょう。
$$\begin{equation}
\begin{split}
x &= \frac{-b+\sqrt{\mathstrut b^2-4ac}}{2a} \\
&=\frac{\sqrt{\mathstrut 4a(\frac{b^2}{4a}-c)}-b}{2a} \\
&=\frac{\sqrt{\mathstrut a}}{a}\cdot\sqrt{\mathstrut \frac{b^2}{4a}-c}-\frac{b}{2a}
\end{split}
\end{equation}$$
ここで
$$\alpha=\frac{\sqrt{\mathstrut a}}{a} \\
\beta=\frac{b^2}{4a} \\
\gamma=\frac{b}{2a}$$
として、α、β、γを事前に求めておけば、次のように式を簡略化することができます。
$$x =\alpha\cdot\sqrt{\mathstrut \beta-c}-\gamma$$
演算が必要になるのは、減算が2回、乗算が1回、平方根が1回です。最初の式に比べると劇的に演算量が減りました。中学校で習う範囲の数学でもここまで最適化が可能になります。
あとは平方根をどうするかが問題となります。平方根の演算は決して軽いものではありません。FPUに平方根演算の命令があればいいのですが、そもそもFPU自体がない場合には、まともに演算しようとすると結構な時間がかかります。
ただ通常は、それでも既成の関数に演算をまかせたほうがよいでしょう。既成の関数の実装がよほど不適切なものであれば、自分で実装し直したほうがよい場合もあり得ます。
もし、精度を落としてもよいのであれば、そして実数の範囲であれば、平方根をさらに高速化する方法はあります。わかりやすい例を挙げましょう。放物線が直線に近い部分に限れば線形近似が可能になります。
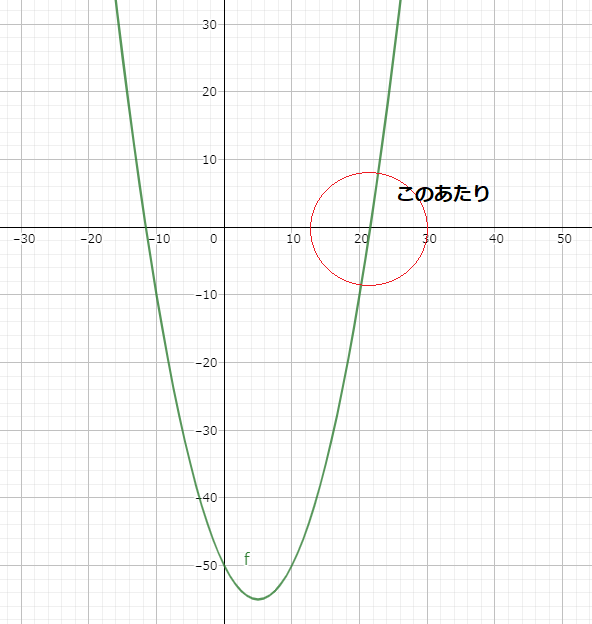
あるいは、表引きと線形補間を用いれば、さらに適用範囲を広げることができることでしょう。しかし、表引きを使う場合は、キャッシュのヒット率なども含めてメモリアクセス速度の影響も受けることになります。
さきほど、「実数の範囲であれば」という但し書きをしました。これは、数値演算は必ずしも実数の範囲とは限らないからです。つまり、虚数の演算もあるということです。
今回取り上げた二次方程式の解の公式に関していえば、平方根の中がマイナスの場合、それを非数(NaN)だといって済ませられるのであればそれでもよいですが、虚数解であっても求めなければならない場合もあるのです。パラメータ自体が虚数(より正確にいえば複素数)のこともあり得ます。
複素数を扱うのであれば、FPUがハードウェア的にサポートしている平方根演算命令は使えないことがほとんどです。そうなると、ソフトウェア的に実装した関数に頼らざるを得なくなりますし、プログラミング言語等によっては自力で関数を実装しなければならないことも出てきます。
このように、いざとなれば手作業による最適化ができるだけの技術を身につけておくのは無駄なことではありません。いや、技術者であれば必ず身につけておくべきでしょう。いざというときにどこまでのことが可能になるかが、その技術者の実力を計るバロメータと考えることもできるのです。


![[迷信] isalpha関数の引数はchar型](https://www.kijineko.co.jp/wp-content/uploads/2021/06/4842077_s.jpg)
![[迷信] コンストラクタから例外を送出してはならない](https://www.kijineko.co.jp/wp-content/uploads/2021/06/2219843_s.jpg)
![[迷信] アルゴリズム関数内で関数オブジェクトはコピーされない](https://www.kijineko.co.jp/wp-content/uploads/2021/06/4845189_s.jpg)
![[迷信] オブジェクトの動的生成に失敗するとメモリリークする](https://www.kijineko.co.jp/wp-content/uploads/2021/06/4673249_s.jpg)
